이직 후로 아직 업무를 본격 시작하기 전이어서 몇 가지 공부하고 있다. 산학 과제 때문에 Bayesian Deep Learning (BDL)을 좀 공부했는데, 카카오에 있을 때부터 이걸 계속 뒤로 미룬 이유를 알 것 같다. 나는 기본적으로 Frequentist여서 Bayesian의 방식을 받아들이기가 너무 어렵다. 여러 강의 자료와 많은 논문을 읽으면서 나름 가장 기초적인 걸 깨우친 듯해서 정리하려 한다. 좀 이상한 점은 BDL이 꽤 많이 연구됐는데, 이를 다룬 Survey 논문을 찾기가 어렵다는 거다. 2~3편이 있긴 한데 분야의 폭과 깊이에 비해서 많이 부족하다. 보통 새로운 분야를 시작할 때 일단 여러 서베이 논문을 읽으면서 그 분야의 전체를 일단 조망하고 필요한 세부 기술을 익히는 방법을 주로 사용하는데, 그런 면에서도 BDL에 익숙해지는 것이 어려웠다. 여러 참고자료를 찾으며 계속 읽으면서 수식에도 약간 익숙해졌지만 아직 그냥 손으로 수식을 막 적을 수 있는 단계도 아니고 이전의 글들과 같이 이 글에도 수식을 따로 넣진 않을 거다.
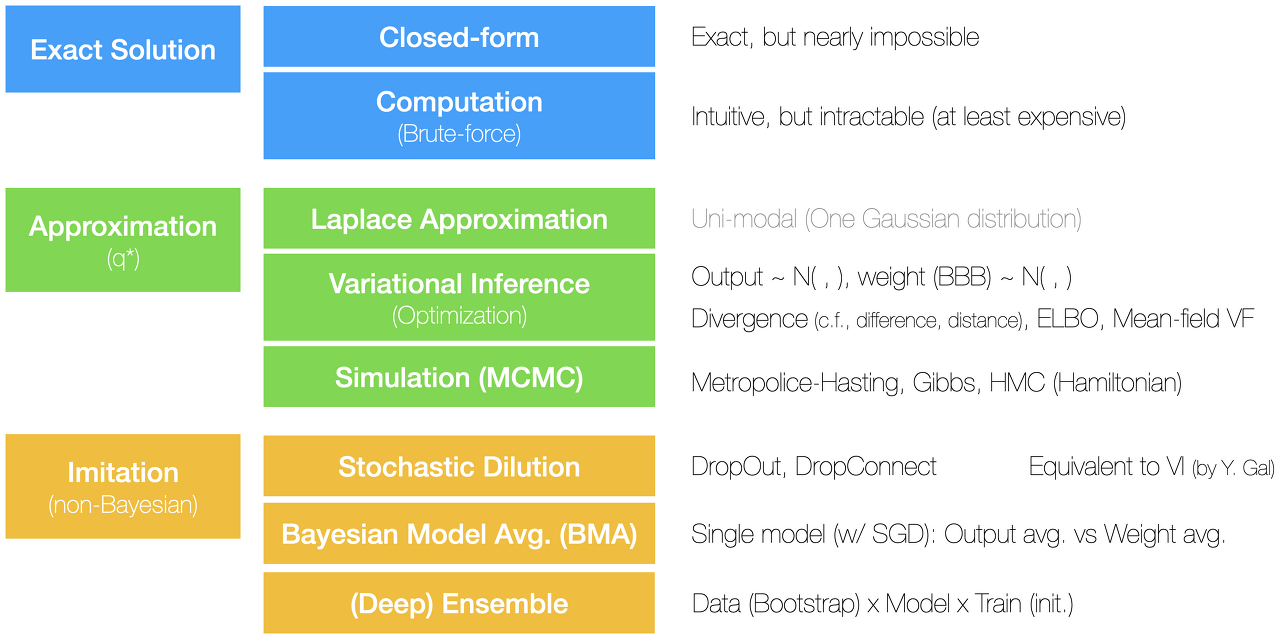
아래 그림과 같이 나름 BDL의 체계를 잡아봤는데, 논란의 여지가 다분하다. 하지만 나름 나의 관점에서 정리한 것이므로 이걸 곧이곧대로 받아들이면 안 된다. BMA는 분명 Bayesian으로 시작하는데, non-Bayesian 하위에 둔 것은 이상해 보이지만 그렇게 한 이유는 뒤에 자세히 설명하겠다. 대부분 존재하는 용어를 가져왔지만 몇몇 용어 (e.g., imitation)는 다른 논문에서 찾아볼 수 없는 것이므로 주의하기 바란다. 앞서 언급했듯이 다양한 서베이 논문이 있으면 이전 저자들의 생각을 바탕으로 또는 종합해서 체계를 만들면 되는데 이번에는 그러지 못해서 상당한 시간을 Bayesian Inference, Variational Inference, MCMC 등의 논문을 여러 편 읽는데 시간을 보냈다.
수식을 안 넣고 싶었지만 아래 수식마저 빠질 수는 없기에 어쩔 수 없이 넣었다. 기본적으로 Bayesian Inference는 주어진 데이터 D가 있을 때, 보이지 않는 모델 파라미터 w의 posterior (사후 확률)을 구하는 거다. 그런데 수식에서 분모에 해당하는 부분, 즉 evidence를 계산하는 것이 대부분의 경우 불가능하다. 그렇기 때문에 위의 그림에 정리한 것과 같은 다양한 방식으로 BDL를 해결한다.
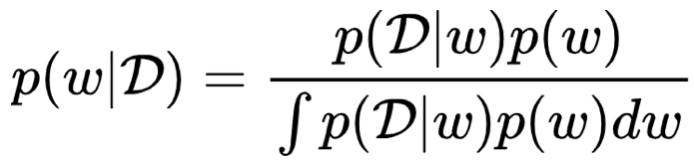
BDL을 해결하는 방식을 크게 3가지로 나눌 수 있다. 1) 정확한 솔루션을 찾거나 2) 사후 확률과 가능한 가깝게 흉내 내거나 3) 베이지언은 아니지만 베이지언인 척 짝퉁을 만드는 거다. 첫 번째 정확한 솔루션을 얻기 위해서 1) 위의 수식을 수학적으로 풀거나 2) 직관적으로 컴퓨터를 이용해서 모든 w에 대해서 분모 evidence의 적분을 구하면 된다. 그런데 이 두 가지가 사실상 불가능하거나 가능하더라도 엄청 비싸기 때문에 정확한 솔루션을 얻는 방법은 없다고 해도 무방하다.
두 번째로 approximation 방식은 1) 라플라스 근사법, 2) variational inference, 그리고 3) MCMC를 이용한 시뮬레이션이 있다. 라플라스 근사법은 — 그림에서 조금 불확실해서 회색으로 적었는데 — uni-modal, 즉 사후 확률이 Gaussian 분포를 따른다는 가정 하에 근사하는 것이므로 일반적인 복잡한 함수를 근사하긴 어렵다. 그래서 특별히 데이터를 잘 설명하지 않는다면 BDL에서 사용하지 않는다고 보면 된다. 초기부터 가장 많이 연구된 방식은 variational inference인데 많은 참고 논문들이 있다. 라플라스 근사법과는 달리 더 복잡한 구조를 추론할 수 있지만 현실적으로 mean field variational family에 속하는 가정 또는 분포만을 사용한다는 한계점이 있다. Approximation을 위해서 원래 분포인 p와 근사 분포인 q* 간의 차이, 즉 divergence를 최소화하도록 q*를 찾는다. 참고로 scalar 값의 차이는 difference, vector 값의 차이는 distance이 듯이, 분포의 차이를 divergence라고 이해하면 된다. 가장 흔히 사용되는 것은 KLD, Kullback-Leibler Divergence가 사용된다. 그런데 이 KLD도 바로 계산하기 어렵기 때문에, ELBO (Evidence Lower BOund)라는 걸 최대화하는 방식으로 q*를 구한다. 아웃풋 값 (y)의 평균과 분산을 바로 구하는 것도 가능하지만, 보통은 모든 파라미터 (w)의 평균과 분산을 구하는 것 (Bayes-By-Backpropagation)이 더 일반적이다. Variational inferece는 다음의 simulation보다는 좀 더 큰 데이터 문제를 해결할 수 있지만, 그럼에도 매우 복잡한 문제를 해결하는 데는 한계가 있다. 보통의 베이지언 추론에서 가장 많이 사용되는 방식은 Markov Chain Monte Carlo 방식의 시뮬레이션을 사용한다. Gibbs 샘플링이 유명하지만 BDL은 메트로폴리스-해스팅 방식을 사용하고, 어떤 논문에서 Hamiltonain MC (HMC)를 사용하기도 한다. 시뮬레이션은 보통의 베이지언 추론을 해결하는 쉬운 방법이지만 데이터 사이즈가 커지고 문제가 복잡해지면 문제 해결 능력에 한계가 있다.
근사법 Approximation이 베이지언 추론에 많이 사용되지만 딥러닝으로 해결해야 하는 문제, 즉 복잡한 모델에선 사용성이 다소 떨어진다. 그래서 일반적으로 non-Bayesian 방식이라 말하는 짝퉁 imitation 방식이 요즘 대세다. 다른 논문에서는 dilution과 BMA를 베이지언 방식 하위에 두기도 하지만, 기본적으로 이 두 방식이 deep ensemble가 별로 다르지 않기 때문에 non-Bayesian에 뒀다. 기본적으로 point estimate인 MLE나 MAP로 구한 네트워크를 활용하기 때문에 non-Bayesian이라 한다. 보통 deep ensemble이 베이지언이 아니라고 말하지만 최근 논문에선 오히려 deep ensemble을 통한 marginalization이 Bayesian을 더 잘 approximate 한다는 주장도 있다. 어쨌든 1) stochastic dilution (일반적인 용어 아님)은 DL에서 regularization에 사용되는 DropOut과 DropConnect를 이용한다. 보통 DO/DC는 학습할 때문 노드나 엣지를 잠시 꺼둠으로써 robust 한 모델을 만들도록 하는데, BDL에선 추론할 때도 DO/DC를 켜 둔다. 즉, 같은 입력값 x를 여러 번 추론하는데, 추론할 때마다 매번 다른 노드/엣지를 꺼두고 결괏값을 계산하고, 그 결괏값들의 분산을 uncertainty로 본다. 그런데 이렇게 구한 값이 Variational Inference의 그것과 다르지 않다고 Yarin Gal이 주장한다. 2) BMA는 Bayesian Model Averaging의 약자로, MLE/MAP로 구한 (로컬) 옵티마의 주변 값들 또는 로컬에서 매번 다시 러닝 레이트를 키워서 새로운 옵티마들을 찾아서 그들의 평균으로 최종 아웃풋을 계산한다. 방식에 따라서 아웃풋의 평균을 취하기도 하고 웨이트 w의 평균을 취해서 결괏값을 계산하기도 한다. 마지막으로 3) Deep Ensemble은 말 그대로 여러 모델을 학습해서 앙상블 하는 방식이다. 기본적으로 동일한 모델/아키텍처에서 초기값을 다르게 해서 여러 모델을 학습해서 평균/분산을 구하지만, 애초에 모델의 종류나 아키텍처를 다르게 한다거나 부트스트랩을 통해서 데이터의 피쳐와 샘플을 다르게 해서 다양한 모델을 만들어서 앙상블 하는 것도 틀렸다고 볼 수 없다. 최근 논문에서 밝혔듯이 deep ensemble이 오히려 더 BDL을 잘 표현한다고 주장하기도 한다. 하지만 딥 앙상블의 최대 단점은 큰 모델을 여러 개 만들어야 하기 때문에 학습 시간이 길어진다는 점이다.
짧게 적으려 했는데 좀 길어졌다. 처음 이 글만을 읽으면 별로 이해에 도움이 되지 않을 거다. BDL 또는 Bayesian Inference에 관심을 갖고 여러 논문을 읽었는데도 잘 이해하지 못했던 분들에게는 다소나마 도움이 되길 바란다. 서두에 밝혔듯이 위의 Taxonomy는 순전히 저의 개인 관점에서 만든 것이므로 이쪽 커뮤니티에서 일반적으로 통용되는 것과는 차이가 있음을 재차 밝힌다. 특히 imitation이나 stochastic dilution (dilution이란 용어는 일반적으로 사용됨) 용어는 이 글에서만 정의된, 일종의 로컬 정의(변수)다. 그리고 위의 체계로 커버하지 못한 다른 많은 방식들이 존재할 수도 있고, 아직은 지식의 끈이 짧아서 잘못 이해하고 적었을 가능성도 있으니 다양한 다른 자료들을 참조해서 스스로 터득하길 바란다.
